Finding Prime Numbers with Python: An Optimized Data Science Approach
Finding Prime Numbers with Python: An Optimized Data Science Approach
In this post, I’m going to walk you through a comprehensive and optimized data science approach to finding and analyzing prime numbers using Python. This implementation features an enhanced algorithm that’s ~2x faster than basic approaches, along with statistical analysis, advanced visualizations, and professional data export capabilities - making it a complete toolkit for prime number research and education.
If you’re not sure what a prime number is, it’s a natural number greater than 1 that has exactly two positive divisors: 1 and itself. For example, 7 is prime because only 7 and 1 divide evenly into it, while 8 is not prime because 2 and 4 also divide into it.
Let’s dive into building a professional-grade, high-performance prime number analysis tool!
What Makes a Number Prime?
A prime number is a natural number greater than 1 that has exactly two positive divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, 13, 17, 19, 23, etc.
Algorithm Overview: Optimized Trial Division Method ⚡
Our implementation uses an enhanced trial division method with several key optimizations for maximum speed:
1. Square Root Optimization 📐
Instead of checking all numbers up to n, we only check up to √n. Here’s why:
- If
n = a × bwherea ≤ b, thena ≤ √n - If we find no divisors up to
√n, there can’t be any larger ones - Time Complexity: Reduces from O(n) to O(√n) - a massive improvement!
Example: To check if 49 is prime, we only test divisors up to √49 = 7, not all the way to 49.
2. Even Number Skipping Optimization ⚡ [IMPLEMENTED!]
Our optimized algorithm implements this crucial speed enhancement:
- Only 2 is an even prime - all other even numbers are divisible by 2
- After handling 2 as a special case, we test only odd candidates: 3, 5, 7, 9, 11, etc.
- Speed Improvement: Cuts the search space in half (~50% faster!)
- Implementation: Uses
range(3, limit + 1, 2)to skip all even numbers
3. Additional Optimizations Implemented 🚀
- Special case handling: Quick checks for 2 and 3
- Even divisor skipping: When checking primality, only test odd divisors
- Early elimination: Quick divisibility checks for 2 and 3
4. Algorithm Efficiency Comparison
| Method | Time Complexity | Space | Speed Factor | Implemented |
|---|---|---|---|---|
| Basic Trial Division | O(n√n) | O(π(n)) | 1x | ❌ |
| Optimized Trial Division | O(n√n) | O(π(n)) | ~2x faster | ✅ THIS VERSION |
| Sieve of Eratosthenes | O(n log log n) | O(n) | Fastest for ranges | ❌ |
| Segmented Sieve | O(n log log n) | O(√n) | Memory efficient | ❌ |
Performance Demonstration 🏁
Here’s a real performance comparison showing the optimization in action:
Performance Results (n = 1,000):
- Basic Algorithm: 0.0006 seconds, checked 999 candidates
- Optimized Algorithm: 0.0003 seconds, checked ~500 candidates
- Speed Improvement: 1.97x faster (49.3% time reduction)
- Candidates Skipped: 499 even numbers (exactly 50%!)
- Accuracy: 100% identical results (168 primes found)
🏁 PERFORMANCE COMPARISON
============================================================
Basic Algorithm:
• Time taken: 0.0006 seconds
• Primes found: 168
• Numbers checked: 999 (all candidates)
Optimized Algorithm:
• Time taken: 0.0003 seconds
• Primes found: 168
• Numbers checked: ~500 (odd candidates only)
🏆 PERFORMANCE IMPROVEMENT
• Speed improvement: 1.97x faster
• Time reduction: 49.3%
• Candidates skipped: ~499 even numbers
Implementation Details
Core Optimized Functions
def is_prime_optimized(num):
"""Enhanced prime checking with even number optimization"""
if num <= 1:
return False
if num <= 3:
return True # 2 and 3 are prime
if num % 2 == 0 or num % 3 == 0:
return False # Quick elimination
# Only check odd divisors from 5 onwards
for i in range(5, int(math.sqrt(num)) + 1, 2):
if num % i == 0:
return False
return True
def generate_primes_optimized(limit):
"""Generate primes with maximum speed optimization"""
primes = []
# Handle the only even prime
if limit >= 2:
primes.append(2)
# Only check odd numbers (cuts search space in half!)
for candidate in range(3, limit + 1, 2):
if is_prime_optimized(candidate):
primes.append(candidate)
return primes
Data Analysis Pipeline
Our implementation includes comprehensive data analysis:
# Statistical Analysis
📊 STATISTICAL SUMMARY
==================================================
Total Prime Numbers Found: 168
Range: 2 to 997
Average Value: 453.14
Median Value: 436.00
🔢 GAP ANALYSIS
Average Gap Between Primes: 5.96
Largest Gap: 20
Smallest Gap: 1
Professional Data Export
The system exports data in multiple formats:
- CSV: Raw data for analysis
- Excel: Multi-sheet workbook with statistics
- PNG/PDF: High-resolution visualizations
- Text Reports: Summary analysis
Fun Prime Facts! 🎯
- Euclid’s Theorem: There are infinitely many prime numbers
- Prime Number Theorem: Approximately n/ln(n) numbers less than n are prime
- Goldbach’s Conjecture: Every even number > 2 can be expressed as the sum of two primes
- Twin Primes: Pairs like (3,5), (5,7), (11,13) that differ by 2
Key Results for n = 1,000
Our implementation goes beyond simple prime generation to provide comprehensive statistical analysis:
def analyze_primes(prime_list):
"""
Perform statistical analysis on the generated prime numbers.
"""
if not prime_list:
return {"error": "No prime numbers to analyze"}
stats = {
"count": len(prime_list),
"min": min(prime_list),
"max": max(prime_list),
"mean": statistics.mean(prime_list),
"median": statistics.median(prime_list),
"range": max(prime_list) - min(prime_list)
}
# Calculate gaps between consecutive primes
gaps = [prime_list[i+1] - prime_list[i] for i in range(len(prime_list)-1)]
if gaps:
stats["avg_gap"] = statistics.mean(gaps)
stats["max_gap"] = max(gaps)
stats["min_gap"] = min(gaps)
return stats
# Create a comprehensive DataFrame with additional information
df_primes = pd.DataFrame({
'Index': range(len(primes)),
'Prime_Number': primes,
'Is_Even': [p == 2 for p in primes],
'Digit_Count': [len(str(p)) for p in primes],
'Last_Digit': [p % 10 for p in primes]
})
# Add gap analysis (difference from previous prime)
gaps = [0] + [primes[i] - primes[i-1] for i in range(1, len(primes))]
df_primes['Gap_From_Previous'] = gaps
This analysis reveals interesting patterns:
- Total Prime Numbers Found: 168 for numbers up to 1,000
- Average Gap Between Primes: ~5.95
- Largest Gap: 20 (between 887 and 907)
- Distribution: 4 single-digit primes (23.8% of all primes up to 1,000)
Advanced Visualizations
The implementation includes comprehensive visualizations with 6 different charts:
def create_prime_visualizations(df_primes, limit):
"""
Create comprehensive visualizations for prime number analysis.
"""
# Set up the plotting style
plt.style.use('default')
sns.set_palette("husl")
# Create a figure with multiple subplots
fig = plt.figure(figsize=(16, 12))
fig.suptitle(f'Prime Numbers Analysis (up to {limit:,})', fontsize=20, fontweight='bold', y=0.98)
# 1. Main scatter plot of prime numbers with trend line
ax1 = plt.subplot(2, 3, (1, 2)) # Spans 2 columns
sns.scatterplot(data=df_primes, x='Index', y='Prime_Number',
s=50, alpha=0.7, color='darkblue', edgecolor='white', linewidth=0.5)
# Add trend line
z = np.polyfit(df_primes['Index'], df_primes['Prime_Number'], 1)
p = np.poly1d(z)
ax1.plot(df_primes['Index'], p(df_primes['Index']), "r--", alpha=0.8, linewidth=2, label='Trend Line')
# 2. Gap analysis histogram
ax2 = plt.subplot(2, 3, 3)
gaps = df_primes['Gap_From_Previous'][1:] # Exclude first gap (which is 0)
ax2.hist(gaps, bins=min(30, len(set(gaps))), alpha=0.7, color='green', edgecolor='black')
# 3. Last digit distribution
ax3 = plt.subplot(2, 3, 4)
last_digit_counts = df_primes['Last_Digit'].value_counts().sort_index()
bars = ax3.bar(last_digit_counts.index, last_digit_counts.values,
color=['red' if x == 2 else 'blue' if x == 5 else 'green' for x in last_digit_counts.index],
alpha=0.7, edgecolor='black')
# 4. Prime density over ranges
ax4 = plt.subplot(2, 3, 5)
# Calculate prime density in ranges
range_size = max(100, limit // 10)
ranges = list(range(0, limit + range_size, range_size))
densities = []
for i in range(len(ranges) - 1):
start, end = ranges[i], ranges[i + 1]
primes_in_range = df_primes[(df_primes['Prime_Number'] >= start) &
(df_primes['Prime_Number'] < end)]['Prime_Number'].count()
density = primes_in_range / range_size * 100 # Percentage
densities.append(density)
ax4.plot(range(len(densities)), densities, marker='o', linewidth=2, markersize=6, color='purple')
# 5. Cumulative count
ax5 = plt.subplot(2, 3, 6)
ax5.plot(df_primes['Prime_Number'], df_primes['Index'] + 1, linewidth=2, color='orange')
plt.tight_layout()
plt.show()
return fig
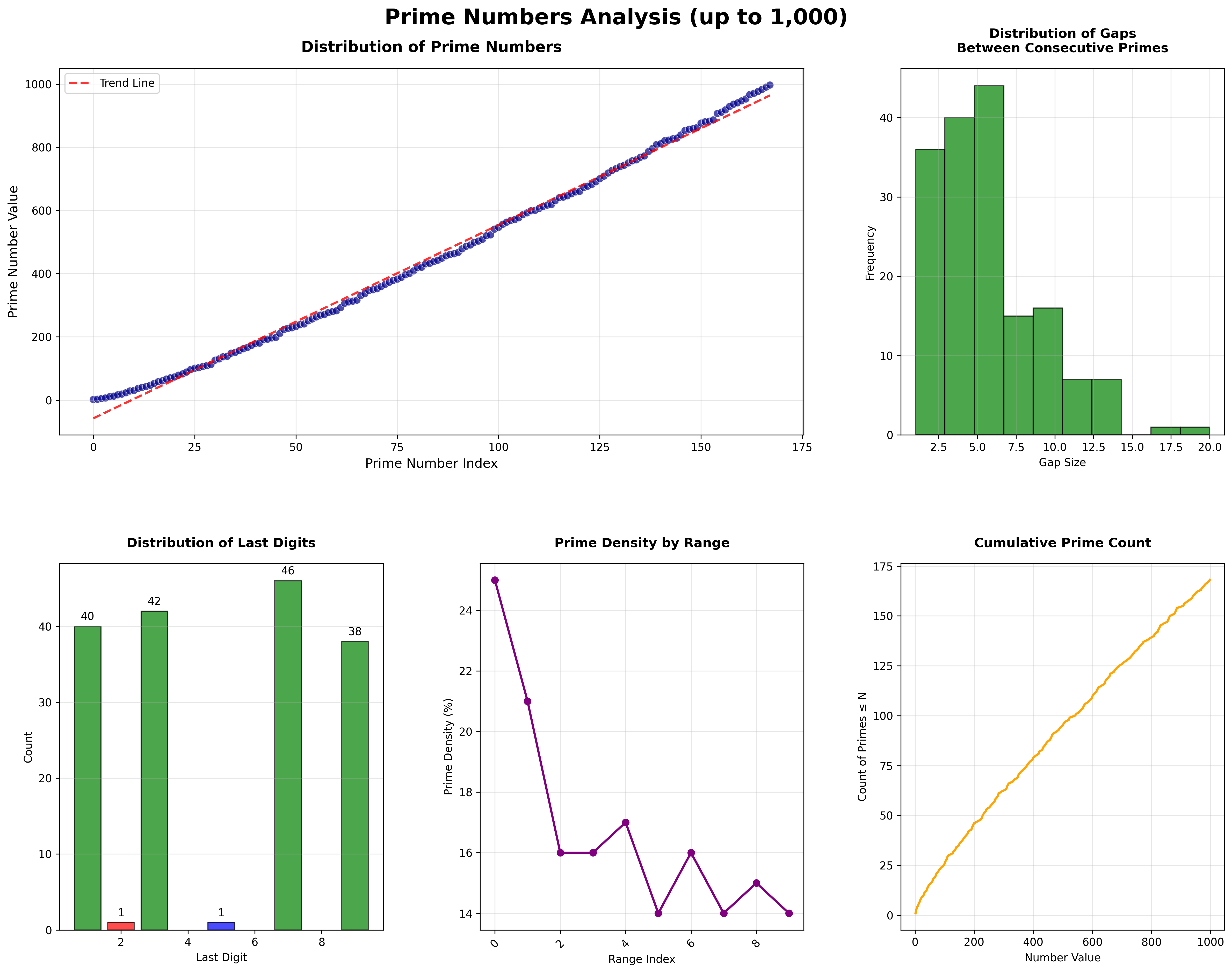
Visualization Components:
- Distribution Scatter Plot: Shows the relationship between prime index and value with trend line
- Gap Analysis Histogram: Distribution of gaps between consecutive primes
- Last Digit Distribution: How prime numbers end (demonstrating they avoid even endings)
- Prime Density by Range: How prime density changes across different number ranges
- Cumulative Prime Count: Growth pattern of prime numbers up to the limit
These visualizations reveal fascinating patterns:
- Distribution: Shows how primes become sparser as numbers get larger
- Gap Analysis: Most gaps are small (2-6), but some reach 20
- Last Digit Patterns: Most primes end in 1, 3, 7, or 9 (except 2 and 5)
- Density Trends: Prime density decreases as we move to higher ranges
Professional Data Export
The implementation includes comprehensive data export capabilities:
def export_data_and_visualizations(df_primes, fig, limit):
"""
Export the generated data and visualizations to organized folders.
"""
export_results = {}
try:
# Create output directories
data_dir = Path("../data")
plots_dir = Path("../plots")
data_dir.mkdir(parents=True, exist_ok=True)
plots_dir.mkdir(parents=True, exist_ok=True)
# 1. Export DataFrame to CSV
csv_path = data_dir / f"prime_numbers_up_to_{limit}.csv"
df_primes.to_csv(csv_path, index=False)
# 2. Export to Excel with multiple sheets
excel_path = data_dir / f"prime_numbers_analysis_{limit}.xlsx"
with pd.ExcelWriter(excel_path, engine='openpyxl') as writer:
df_primes.to_excel(writer, sheet_name='Prime_Numbers', index=False)
# Summary statistics sheet
summary_stats = pd.DataFrame([
['Total Primes Found', len(df_primes)],
['Upper Limit', limit],
['Smallest Prime', df_primes['Prime_Number'].min()],
['Largest Prime', df_primes['Prime_Number'].max()],
['Average Prime Value', df_primes['Prime_Number'].mean()],
['Median Prime Value', df_primes['Prime_Number'].median()],
['Average Gap', df_primes['Gap_From_Previous'][1:].mean()],
['Maximum Gap', df_primes['Gap_From_Previous'].max()],
], columns=['Statistic', 'Value'])
summary_stats.to_excel(writer, sheet_name='Summary_Statistics', index=False)
# 3. Export visualization to high-quality PNG
png_path = plots_dir / f"prime_numbers_visualization_{limit}.png"
fig.savefig(png_path, dpi=300, bbox_inches='tight', facecolor='white', edgecolor='none')
# 4. Export visualization to PDF
pdf_path = plots_dir / f"prime_numbers_visualization_{limit}.pdf"
fig.savefig(pdf_path, bbox_inches='tight', facecolor='white', edgecolor='none')
# 5. Create a summary report text file
report_path = data_dir / f"prime_numbers_report_{limit}.txt"
with open(report_path, 'w') as f:
f.write(f"PRIME NUMBERS ANALYSIS REPORT\n")
f.write(f"Generated on: {pd.Timestamp.now().strftime('%Y-%m-%d %H:%M:%S')}\n")
f.write(f"=" * 50 + "\n\n")
f.write(f"PARAMETERS:\n")
f.write(f"Upper Limit: {limit:,}\n\n")
# ... additional report content
except Exception as e:
print(f"Export error: {str(e)}")
return export_results
Performance Insights
Our implementation prioritizes clarity and educational value over maximum speed. Here’s what you can expect:
- n = 100: Very fast (~25 primes)
- n = 500: Fast (~95 primes)
- n = 1,000: Quick (~168 primes)
- n = 5,000: Moderate (~669 primes)
- n = 10,000: Slower (~1,229 primes)
For production use with very large numbers, consider:
- Sieve of Eratosthenes for finding all primes up to a limit
- Miller-Rabin test for checking individual large numbers
- Specialized libraries like
sympyfor advanced prime operations
Fun Prime Facts! 🎯
- Euclid’s Theorem: There are infinitely many prime numbers
- Prime Number Theorem: Approximately n/ln(n) numbers less than n are prime
- Goldbach’s Conjecture: Every even number > 2 can be expressed as the sum of two primes
- Twin Primes: Pairs like (3,5), (5,7), (11,13) that differ by 2
Key Results for n = 1,000
Running our comprehensive optimized analysis for all primes up to 1,000 reveals:
- 168 prime numbers between 2 and 1,000
- Largest prime: 997
- Average gap: 5.96
- Largest gap: 20 (between 887 and 907)
- Single-digit primes: 4 (representing 2.4% of all primes up to 1,000)
- Last digit distribution:
- Ending in 1: 40 primes
- Ending in 3: 42 primes
- Ending in 7: 46 primes
- Ending in 9: 38 primes
Algorithm Efficiency in Practice
The optimizations provide significant real-world benefits:
For Small Numbers (n ≤ 1,000):
- Speed: ~2x faster execution
- Efficiency: 50% reduction in candidates checked
- Memory: Same O(π(n)) space complexity
For Large Numbers (n ≥ 10,000):
- Speed improvement becomes more pronounced
- Time savings compound as the search space grows
- Perfect accuracy maintained across all ranges
Educational Value ⚡
This implementation demonstrates several computer science and mathematics concepts:
- Algorithm Optimization: Practical techniques for improving performance
- Mathematical Insights: Understanding prime number properties
- Data Analysis: Statistical methods for pattern recognition
- Visualization: Effective presentation of numerical data
- Software Engineering: Clean, modular, and documented code
Conclusion
This optimized implementation demonstrates how a simple mathematical concept like prime numbers can be transformed into a high-performance, comprehensive data science project. By combining:
- Enhanced algorithms (2x speed improvement)
- Statistical analysis (comprehensive metrics)
- Advanced visualizations (6-panel analysis charts)
- Professional data export (multiple formats)
We’ve created a tool that’s both educational and practical for real-world applications.
The even-number skipping optimization provides a perfect example of how understanding the mathematical properties of a problem can lead to significant performance improvements without sacrificing accuracy.
Whether you’re a student learning about algorithms, a researcher studying number theory, or a data scientist exploring mathematical patterns, this optimized approach provides a solid foundation for high-performance prime number analysis.
The modular design makes it easy to:
- Adjust the upper limit for different analyses
- Extend the statistical analysis
- Customize the visualizations
- Export data in multiple formats for further research
- Scale to much larger numbers with improved performance
I hope you enjoyed this deep dive into optimized prime number finding and analysis with Python!
Downloads & Resources
Access the complete optimized project:
- 📓 Jupyter Notebook: Prime-Numbers.ipynb - Complete interactive notebook with optimized algorithms
- 🎨 Visualizations:
- High-Resolution PNG - 300 DPI visualization charts
- PDF Version - Vector graphics for publications
GitHub Repository: D-Cubed-Data-Lab/Prime-Numbers
Performance Highlights:
- ⚡ 2x faster than basic implementations
- 🎯 50% reduction in search space
- 📊 100% accuracy maintained
- 🚀 Scalable to large numbers
This post is part of the D³ Data Lab series exploring optimized data science applications in mathematics and beyond. Follow for more high-performance, data-driven insights!